Fibonacci Sequence John Canessa
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, , 144, 233, 377 Fibonacci Sequence Formula The formula for the Fibonacci Sequence to calculate a single Fibonacci Number is \ F_{n}={\dfrac{(1\sqrt{5})^{n}(1\sqrt{5})^{n}}{2^{n}\sqrt{5}}} \ or F n = ( (1 √5)^n (1 √5)^n ) / (2^n × √5) for positive and negative integers nFind sum of 5*()/3^(n2) (5 multiply by (1 plus 1 plus 2 plus 3 plus 5 plus 8 plus 13 plus 21 plus 34 plus 55 plus plus 144 plus 233 plus 377 plus 610) divide by 3 to the power of (n minus 2)) series How to calculate sigma Sum of n terms of the sequence converges or diverges THERE'S THE ANSWER!
One 2 3 4 5 6 7
One 2 3 4 5 6 7-1, 1, 2, 3, 5, 8, 13, 21, 34, 55, , 144, _233_, _377_, _610_ Explain the pattern used to find the remaining numbers for the sequence The final term in the sequence is added to the previous term to get the next termFibonacci(7) = 5 8 = 13 Fibonacci(8) = 8 13 = 21 Fibonacci(9) = 13 21 = 34 Fibonacci(10) = 21 34 = 55 Fibonacci(11) = 34 55 = Fibonacci(12) = 55 = 144 Fibonacci(13) = 144 = 233 Fibonacci(14) = 144 233 = 377 The output statements in the flowchart show the value of i and the Fibonacci number fib You would print or
1 Data The First Fifteen Fibonacci Numbers Are 1 Gauthmath
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, Note In this video tutorial we've taken 0 and 1 as the first 2 numbers in the Fibonacci series they're called Seed Values And we ask the user to enter the limit or the number of terms to be printed in the Fibonacci Series0,1,1,2,3,5,8,13,21,34,55,,144, 233,377 to infinity and beyond!1) Which number is next in the Fibonacci sequence of numbers 1, 1, 2, 3, 5, 8, 13, 21 a) 55 b) 34 c) 8 d) 162 2) Which of the following is NOT an example of Fibonacci numbers found in nature?
Only nerds and people who use google will get thisFibonacci Numbers We begin our whirlwind tour of F Lo Sophia and Sacred Geometry by first stopping in Pisa, Italy, where in the year 12 AD (or as currently written, CE for "Current Era"), a mathematician and merchant, Leonardo da Pisa wrote a book, Liber Abaci (The Book of Computation) Born in 1179, Leo had traveled during the last years of the 12th century to Algiers1) Fibonacci Series Write a c# program to print fibonacci series without using recursion and using recursion Input 15 Output 0 1 1 2 3 5 8 13 21 34 55 144 233 377
One 2 3 4 5 6 7のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
Fibonacci Marketing |  Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing | Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing | Fibonacci Marketing | Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing | 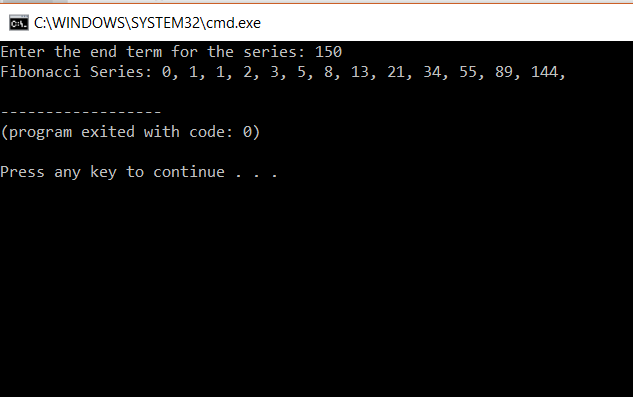 Fibonacci Marketing |
 Fibonacci Marketing | Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing | Fibonacci Marketing |  Fibonacci Marketing |
Fibonacci Marketing |  Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing | Fibonacci Marketing |
 Fibonacci Marketing | 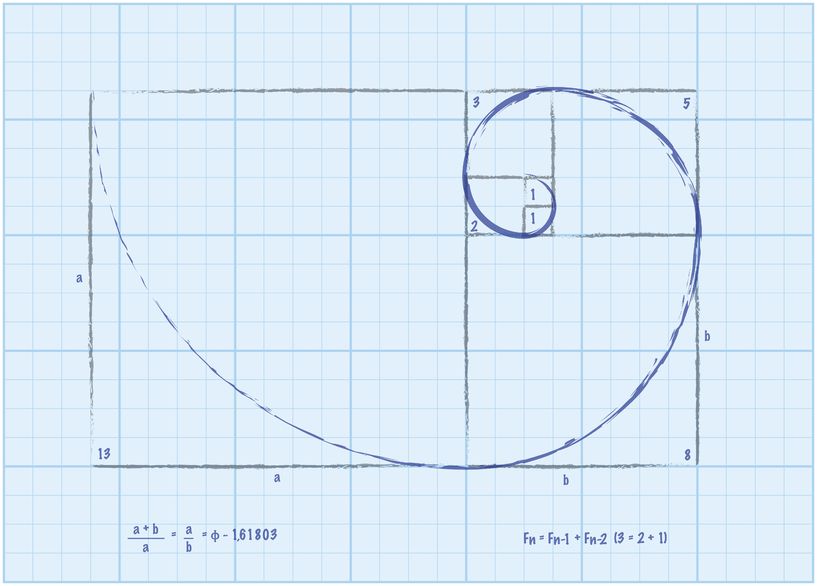 Fibonacci Marketing |  Fibonacci Marketing |
Fibonacci Marketing | Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing | Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing | Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing | 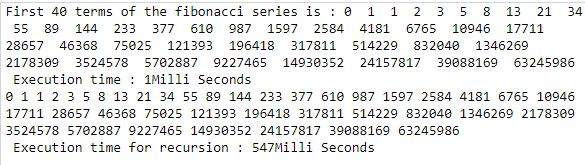 Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing | 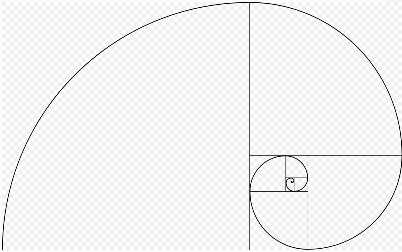 Fibonacci Marketing |
 Fibonacci Marketing | Fibonacci Marketing | 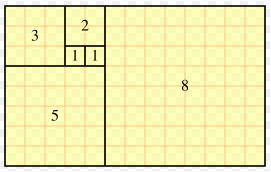 Fibonacci Marketing |
 Fibonacci Marketing | 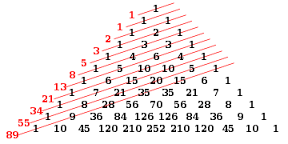 Fibonacci Marketing | Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing | Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing | 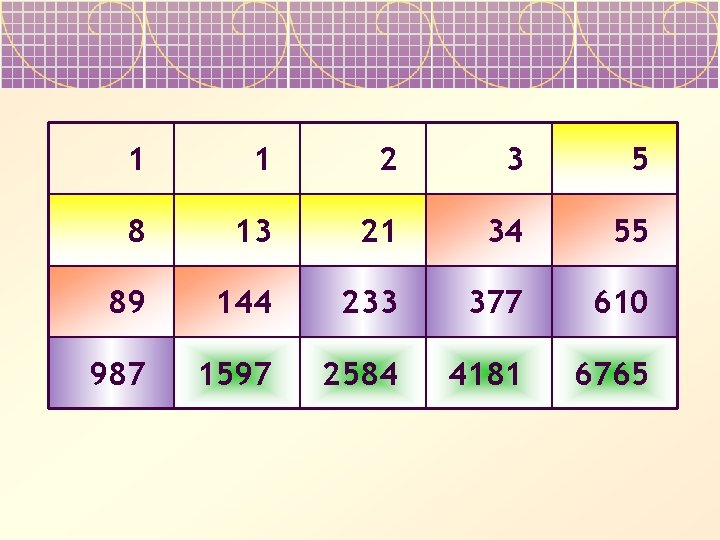 Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing | 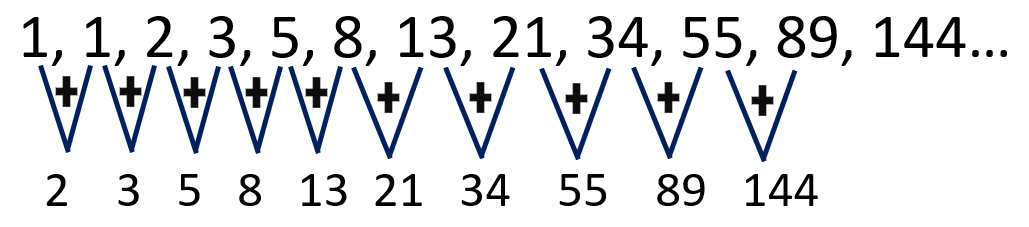 Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing |  Fibonacci Marketing |
Fibonacci Marketing |  Fibonacci Marketing | Fibonacci Marketing |
 Fibonacci Marketing |  Fibonacci Marketing | 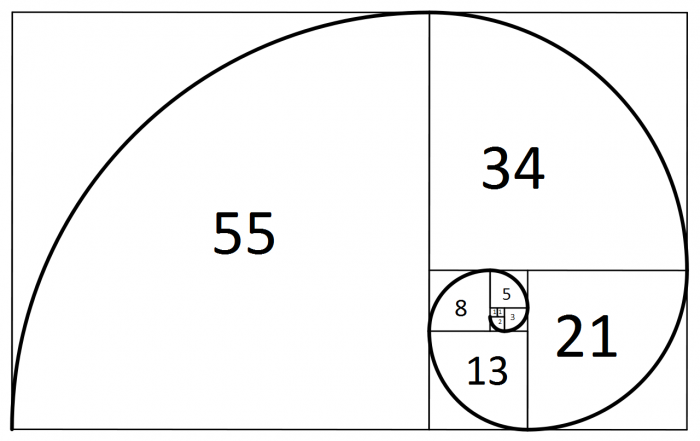 Fibonacci Marketing |
Fibonacci Marketing |  Fibonacci Marketing |  Fibonacci Marketing |
Fibonacci Marketing |  Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing | Fibonacci Marketing |  Fibonacci Marketing |
 Fibonacci Marketing |
This sequence is the famous fibonacci's sequence, where each number is the sum of the last two The sequence given starts off a little later, as the series starts at 0, and 1 0, 1, 1 (1 0), 2 (11), 3Does these ratios seem to be converging to any particular number?
Incoming Term: 1 1 2 3 5 8 13 21 34 55 89 144 233, 0 1 1 2 3 5 8 13 21 34 55 89 144, search 1 2 3 4 5 6, one 1 2 3 4 5 6, search 1 2 3 4 5, one 2 3 4 5 6 7,



